Открытые и замкнутые алгебры
Открытые алгебры
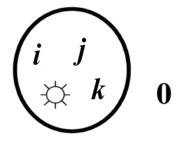
Естественно, что свою роль единицы в «сложных» алгебрах не теряют. На примере рисунка во взаимодействии находятся два пространства, но так, что в «умножении» четыре полярностей с единицей ☼, а в «сложении» пять полярностей с единицей 0 (ноль).
Алгебра над таким полем в интенсивности связи (операциях) «умножения» будет: ί*j*k = ί2 = j2 = k2 = ☼, ί*j = k, ί*k = j, j*k = ί.
В интенсивности связи «сложения» ί + j + k + ☼ = 0.
К примеру, (ί + j + k)2 = 3☼ +2(ί + j + k) =1, так как в количественном смысле ☼ = 1. Не трудно заметить, что в «сложении» современная алгебра не указывает «постановку в соответствие». Например, + а + а + а + а так и оставляют, без постановки этим взаимодействиям в соответствие один или несколько полярных объектов. Напомню, что в «умножении», например (–)(–)(–)(–) = +.
Замкнутые алгебры
В современной алгебре цикличным является только «умножение». Например, (–)(–) = +, но (–)(–)(–) = (–) . Точно так же в «комплексных числах» ί4 = +, но ί5 = ί.
Однако системы «сложения» тоже могут быть замкнутыми. Для этого и в сложении должна быть цикличность. Некоторым образом в арифметике десятеричной системе есть цикл, когда после числа 10 счёт повторяется. Однако для поляризованных объектов цикличность может быть такой, что (–1) + (–1) = 0, (+1) + (+1) = 0.
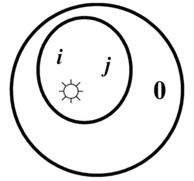
Более наглядно это выполнено без противоречий в системе, где три полярных объекта ί, j, ☼ в «умножении» и четыре полярных объекта ί, j, ☼, 0 в «сложении». Итак, в «умножении» ί2 = j, j2= ί, ί*j =☼, ί3 = j3 = ☼,
В «сложении» ί + j + ☼ = 0, ί + j = ☼, ί + ☼ = j, j + ☼ = ί, 2ί = 2 j = 2☼ = 0. Так как в количествах ☼ ≡ 1, то 1 + 1 = 0.
Возьмём теперь в пример суперпозиционную локу, где ί*j*k = ί2 = j2 = k2 = ☼, ί*j = k, ί*k = j, j*k = ί. В интенсивности связи «сложения» ί + j + k + ☼ = 0.
Будет ί + j + k = ☼ и далее ☼2 = 3☼ + 2☼, то есть 3☼ + ☼ = 0. Так как в отношениях полярность класса ☼ принимает единичность, то 1 + 1 + 1 + 1 = 0.
Такой «абсурд» не получают в современной алгебре «действительных чисел» лишь потому, что изначально пространство «сложения» не определяет группу и не допускает взаимодействие полярного объекта с самим собой. Если бы в группе «сложение» из трёх полярных объектов +, – , 0 допущено было взаимоотношения полярности с самой собой, то не трудно доказать, что (–) + (–) = +, (+) + (+) = –, (+) + (–) = 0.
В понятных терминах, (–1) + (–1) = +1, (+1) + (+1) = –1, (+1) + (–1) = 0, то есть 2(–)= +, 2(+) = –. Однако, во избежание противоречия, пространство «сложения» пришлось бы увеличить ещё на одну полярность.
Следует всегда помнить различие между единицей как качеством, охватывающим класс в тождественные объекты, и единицей, как количеством, обусловленным присутствием этой единицы в каждом объекте. Например, единица как класс ☼, по сути, и есть 1 как количество. Точно так же 0, как класс, содержится и тождественен в 0, как количество этого класса.
Классы с «нулевой» единицей принято называть «сложением», а с ☼ – «умножением». Естественно, что единицы могут отличаться от известных. При этом появляются пространства с соответствующей интенсивностью связи.
Примечание:
В простых алгебрах интенсивность связи одна и та же и, соответственно, единица в них всеобщая. Для пространств, находящихся во взаимодействии с одной интенсивностью связи нет необходимости её указывать. Единицу можно выбирать любую.
В сложных алгебрах, или когда полагаются пространства с иной интенсивностью связи, единица определяется четко и соответственно виду интенсивности связи.
По приведённому рисунку в пространстве с интенсивностью «сложение» будет ί + j + ☼ = 0. В пространстве «умножение» ί*j =☼. В приведённом примере пространство «умножения» на одну полярность меньше пространства «сложения».
Образ такого есть в современной алгебре, где (+1) + (–1) = 0 имеет три полярности, но (–)*(–) = + только две полярности.
Конечно, произвола в алгебрах нет. Не каждый вид пространств войдёт в соотношение по интенсивностям связей без противоречий.