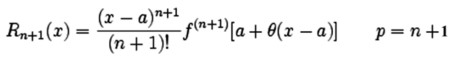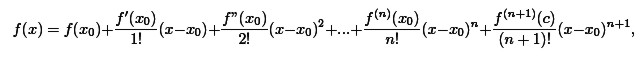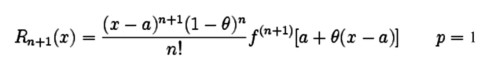Разложение функций в ряд: различия между версиями
Admin (обсуждение | вклад) (Новая: Оценим возможности рядов. 1. Полярность в ряд разложить нельзя. Её можно получить взаимоотношениями ...) |
Admin (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
некоторой окрестности точки <span style="color:blue"><big>''a''</big></span> , тогда ряд | некоторой окрестности точки <span style="color:blue"><big>''a''</big></span> , тогда ряд | ||
| − | [[Изображение: | + | [[Изображение:math_fileP1.jpg]] |
называется рядом Тейлора функции <span style="color:blue"><big>''f''</big></span> в точке <span style="color:blue"><big>''a''</big></span>. | называется рядом Тейлора функции <span style="color:blue"><big>''f''</big></span> в точке <span style="color:blue"><big>''a''</big></span>. | ||
| Строка 30: | Строка 30: | ||
В форме Лагранжа: | В форме Лагранжа: | ||
| − | [[Изображение: | + | [[Изображение:math_fileP2.jpg]] |
Тогда формула Тейлора с остаточным членом в форме Лагранжа будет: | Тогда формула Тейлора с остаточным членом в форме Лагранжа будет: | ||
| − | [[Изображение: | + | [[Изображение:math_fileP5.jpg]] |
где | где | ||
| − | [[Изображение: | + | [[Изображение:math_fileP51.jpg]] |
В форме Коши: | В форме Коши: | ||
| − | [[Изображение: | + | [[Изображение:math_fileP3.jpg]] |
Изменим предположения: | Изменим предположения: | ||
| Строка 51: | Строка 51: | ||
тогда: | тогда: | ||
| − | [[Изображение: | + | [[Изображение:math_fileР4.jpg]] |
- остаточный член в форме Пеано. | - остаточный член в форме Пеано. | ||
Текущая версия на 10:54, 16 февраля 2009
Оценим возможности рядов.
1. Полярность в ряд разложить нельзя. Её можно получить взаимоотношениями других полярностей, а это – алгебра.
2. В ряд можно разложить только однополярные количества.
3. По этим причинам современные функциональные ряды следует пересмотреть.
Вот пример сегодняшнего определения: Ряд Тейлора — разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора.
Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a , тогда ряд
называется рядом Тейлора функции f в точке a.
В случае, если a = 0, то этот ряд называется рядом Маклорена.
Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.
Как видим, некоторое a получило полярность.
Более того, есть ещё «остаточные члены»:
Остаточные члены в форме Лагранжа, Коши и Пеано
В форме Лагранжа:
Тогда формула Тейлора с остаточным членом в форме Лагранжа будет:
В форме Коши:
Изменим предположения:
• Пусть функция f (x) имеет n – 1 производную в некоторой окрестности точки a
• Пусть n имеет производную в самой точке a,
тогда:
- остаточный член в форме Пеано.