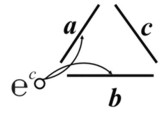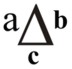Пространство и время

Случайно ли физики-исследователи стали погружаться в микромир?

С одной стороны, их линейный ум полагал первопричину а «микромире». Эта идея ума заключена в том, что есть изначальные «кирпичики», из которых складываются «крупные» объекты. Это и есть основное свойство линейного ума – нахождение причин по следствию.

С другой стороны, по мере углубления к «первопричинам» масса объектов уменьшается.

Человек может создать и найти только то, что представляет собой. Если воспринимать нечем, то и темы нет. Поэтому любую задачу и пищу уму подают органы непосредственного восприятия. Анализатором, например зрения, массу объекта не определить; опыт массы идёт от осязания. Следовательно, задача может быть поставлена наоборот: как достичь, к примеру, свойствами анализатора осязания, свойств анализатора зрения.

Итак, устремляясь к уменьшению массы объектов, исследователи стали приближаться к свойствам звука и света.

Звук имеет частотные характеристики. Поэтому найдены «волновые» процессы.

Масса света отсутствует. Вот тут и начались парадоксы и ломка привычек к большим массам.

В трёхполярном пространстве линейности нет, и объект может находиться сразу в двух полярных возможностях этого пространства. Этого лишены «крупные» объекты по причине своей поляризации. Например, Земля обладает магнитным полем, а, следовательно, носит четырёхполярную поляризацию. Поэтому для Земли, как для «крупного» тела есть своё время и своё пространство.

Что происходит в трёхполярном пространстве? Время там, в обычном понятии, не существует. Теперь представим, что объект попадает в это пространство…

Вот тут и начинается стихия изысканий и каламбур трактовок, в которые попадают исследователи, имеющие линейный ум. Получается вполне реально, что пространство и время относительные, и вовсе не зависят от некоторой линейной скорости, приближающейся к скорости света, как полагает Теория Относительности, исходя из двухполярной алгебры преобразований Лоренца.

Впрочем, какова алгебра, таковы и результаты. Однако в приведённом случае ни алгебра "действительных чисел" (как в преобразованиях Лоренца, применённых в Теории Относительности), "ни алгебра функций комплексных переменных" (как в уравнении Шрёдингера) не пригодны.

Если взять отношение трёх полярностей, то запишем

= a/b/c = (a)(b)ⁱ(c)^j.

Здесь a одновременно относится и к b и к c, точно так же, как b одновременно относится и к a и к c. Возьмём для примера трёхполярное умножение ί j k = 1.

Здесь в сложении ί + j + k = 0.

Это возможно и непротиворечиво, когда ί = j k, j = ί k, k = ί j .

Отсюда ί² = j² = k² = 1. На базе этого в сложении получим ί² + j² + k² = 0, а так же ί² + j² + k² + 2(ί + j + k) = 0. В итоге, 3 = 0. Не спешите с выводом, это не противоречие. В подобных пространствах ί + j = k, ί + k = j, j + k = ί. В итоге получим цикличность не только в умножении, но и сложении, когда 2ί = 2j = 2k = 0, но 3ί = ί, 3 j = j, 3k = k.

Что показывает такая алгебра?

Прежде всего в уравнении волновой функции (как в уравнении Шрёдингера) будет три (а не два) сопряженных выражения. Уже это даст иные результаты (на сопоставлении с уравнением Шрёдингера) состояний объектов, попавших в трёхполярное пространство.

Во вторых, время "закорачивается" с чёткой величиной искажения.

В третьих, пространство "искривляется так, что объект одновременно присутствует в двух разобщённых точках.

В четвёртых, это означает возможность клонирования объектов.

Подробнее смотрите в разделе Волновой функции и Многополярные алгебры.